1074. Number of Submatrices That Sum to Target (Hard)

更新于 阅读次数： 本文字数： 4.2k 阅读时长 ≈ 4 分钟

矩阵求和问题。给定一个矩阵 matrix 和一个目标值 target，求和为 target 的子矩阵的数量。

这是典型的前缀和应用场景，我们分别用两种思路应用前缀和来解决这个问题。

Understanding the Problem

With solutions both in Python and Java.

这是一道困难题，先读题。

Given a matrix and a target, return the number of non-empty submatrices that sum to target.

A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.

Two submatrices (x1, y1, x2, y2) and (x1', y1', x2', y2') are different if they have some coordinate that is different: for example, if x1 != x1'.

理解一下。

  • 参数是 1 个矩阵，一个目标值；
  • 需要返回的是子矩阵的数量，这些子矩阵需要满足：
    • 非空；
    • 和等于目标值。

看看例子。

Example 1:

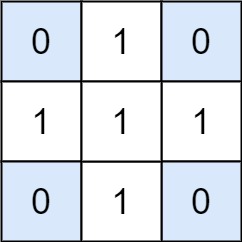
1074.eg.jpg

Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
Output: 4
Explanation: The four 1x1 submatrices that only contain 0.

这个例子中矩阵如图，需要找出所有和为 0 的子矩阵。可见只有四个角的元素满足，这四个子矩阵只能有一个元素。

Example 2:

Input: matrix = [[1,-1],[-1,1]], target = 0
Output: 5
Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.
y1 y2
x1 1 -1
x2 -1 1

这个例子中，所有元素字面量都不为 0，所以排除 1x1 子矩阵之后，只有尺寸为 2x1 / 1x2 和 2x2 的子矩阵的和可能为 0。

我们来输出一下 2 个元素的组合（2x1/1x2），去除对角线的两种不满足条件的组合，可以发现剩余的四种组合的和都为 0。而唯一一种 2x2 的组合我们也能一眼看出来其和为 0，所以这个例子的答案是 5。

>>> [(x, sum(x)) for x in combinations([1,-1,1,-1], 2)]
[((1, -1), 0), ((1, 1), 2), ((1, -1), 0), ((-1, 1), 0), ((-1, -1), -2), ((1, -1), 0)]

Example 3:

Input: matrix = [[904]], target = 0
Output: 0

当不存在满足条件的子矩阵时返回 0。

这道题的限制条件比较重要。

Constraints:

  • 1 <= matrix.length <= 100
  • 1 <= matrix[0].length <= 100
  • -1000 <= matrix[i] <= 1000
  • -10^8 <= target <= 10^8

矩阵的尺寸从最小一个元素到最大 100*100 个元素，并且元素的值可能为负数，这意味着没有取巧的办法，对于每一种子矩阵的组合我们都必须算出和才能断定是否符合条件。

思路 & Solutions

递归方法（X 超时）

乍一看题可能你会感觉没有思路，难道只能：

  • 遍历长宽得出所有子矩阵尺寸；
  • 遍历每种尺寸去匹配可能出现的子矩阵，硬算矩阵和。

（没错，我一开始这样做的…）

这样确实可以计算出答案，问题是计算量指数爆炸，100*100 的 input 必然超过时间限制。

动态规划（DP）

仔细一看这道题有给一个提示，也别客气直接来看看提示。

Using a 2D prefix sum, we can query the sum of any submatrix in O(1) time. Now for each (r1, r2), we can find the largest sum of a submatrix that uses every row in [r1, r2] in linear time using a sliding window.

提示给出的思路分为两步：

  • 求出矩阵每个元素的前缀和（prefix sum），这一步时间复杂度是 O(n)，但是后续查询某个子矩阵的和只需要 O(1)；
  • 用滑动窗口（Sliding Window）遍历每一个子矩阵，检查和是否等于目标值。

要应用这个思路，我们可以得到两种方法。

方法一，计算矩阵所有元素的前缀和

  • 首先计算矩阵所有元素的前缀和；
    • prefixSum[x][y] = matrix[x][y] + prefixSum[x-1][y] + prefixSum[x][y-1] - prefixSum[x-1][y-1]
      • prefixSum[x][y] -> 以(0, 0)为左上角，矩阵中对应位置为右下角的子矩阵的和；
      • matrix[x][y] -> 矩阵对应位置的元素的值；
      • prefixSum[x-1][y] -> 矩阵上一行同列的值，这个值已经计算过了；
      • prefixSum[x][y-1] -> 矩阵上一列同行的值，这个值也已经计算过了；
      • prefixSum[x-1][y-1] -> 需要注意的是，这个值在上面两个子矩阵中被计算了两次，所以这里减去一次。
  • 使用滑动窗口来遍历行或列；
    • 比如当遍历行时，对于 (r1, r2) （即第一行和第二行中的子矩阵）的情况，我们逐列遍历：
      • 初始化一个哈希表，初始化 key 为 0 时的值为 1，这一步是为了处理子矩阵的和刚好为目标值的情况；
      • 我们查询 ((0,0), (1, 1)) 的和，并检查这个和减去目标值后的值在哈希表中对应的值；
        • 子矩阵的和减去目标值后的数，其实就是之前记录过的和为该值的子矩阵；
        • 如果存在的话，那么意味着现在检查的这个子矩阵减去这个子矩阵，就能得到一个满足条件的子矩阵；
        • 由于在下一步我们按列将每次检查的结果存入列哈希表中，哈希表的 key 对应的值是指 key 出现的次数；
        • 这也就意味着如果同一个值出现了多次，那么就存在这么多子矩阵可以满足条件，所以我们将答案加上哈希表中对应的次数。
      • 将其作为 key 存入一个哈希表中，将值+1（key 不存在的情况设为 1）；
      • 对行的组合重复这一步。

下面是 Java 代码可以配合理解。

class Solution {
    public int numSubmatrixSumTarget(int[][] matrix, int target) {
        int rows = matrix.length,
            cols = matrix[0].length,
            ans = 0;

        // 初始化一个前缀和2D数组
        int[][] prefixSum = new int[rows][cols];

        // 为避免处理数组越界，我们对第一行数据单独进行遍历
        prefixSum[0][0] = matrix[0][0];
        for (int c = 1; c < cols; c++) {
            // 对于第一行数据，当前值加等于前一个值
            prefixSum[0][c] = prefixSum[0][c-1] + matrix[0][c];
        }

        // 剩下的数据逐行逐列遍历
        for (int r = 1; r < rows; r++) {
            for (int c = 0; c < cols; c++) {
                // 对应位置的前缀和等于上一行对应位置的值和上一列对应位置的值之和，减去重复计算的区域的值
                prefixSum[r][c] = matrix[r][c] + prefixSum[r-1][c]
                    + (c == 0 ? 0 : prefixSum[r][c-1] - prefixSum[r-1][c-1]);
            }
        }

        // 计算完前缀和，我们对行进行组合遍历
        for (int sr = 0; sr < rows; sr++) {
            for (int er = sr; er < rows; er++) {
                // 初始化一个哈希表来存储次数
                Map<Integer, Integer> map = new HashMap<>();
                map.put(0, 1);
                for (int c = 0; c < cols; c++) {
                    // 计算第一列到当前列组成的矩阵的和
                    int cur = prefixSum[er][c] - (sr == 0 ? 0 : prefixSum[sr-1][c]);
                    // 查询当前窗口中，需要减去的矩阵是否存在/存在几个
                    if (map.get(cur - target) != null) {
                        ans += map.get(cur - target);
                    }
                    // 将当前矩阵的值存入哈希表，将次数+1
                    map.put(cur, map.get(cur) == null ? 1 : map.get(cur) + 1);
                }
            }
        }

        return ans;
    }
}

方法二，仅按行或列计算前缀和

  • 与方法一最大的区别在于，方法二不去计算一个 2D 矩阵的前缀和，而是逐行计算这一行的前缀和；
  • 这个前缀和数组由循环外部的变量，变成列循环内部的变量，随着基础行的变化而重置；
  • 除去计算前缀和的变化，在滑动窗口内的操作与方法一一致，因此降低了空间复杂度。

下面是 Python 帮助理解。

class Solution:
    def numSubmatrixSumTarget(self, matrix: List[List[int]], target: int) -> int:
        rows, cols, ans = len(matrix), len(matrix[0]), 0

        for sr in range(rows):
            colsum = [0] * cols
            for er in range(sr, rows):
                d, cur = {0:1}, 0
                for c in range(cols):
                    colsum[c] += matrix[er][c]
                    cur += colsum[c]
                    ans += d.get(cur-target, 0)
                    d[cur] = d.get(cur, 0) + 1

        return ans

总结

这是一道困难的题，难点在于把计算计划到规定的复杂度中。

要得到答案，需要一些前置的知识：

  • 前缀和的应用；
  • 动态规划的应用；
  • 滑动窗口的应用。
相关文章